利用地震成像方法准确重建近地表速度结构有助于开展高精度地震勘探、探查浅部矿产资源、规避潜在自然灾害,并利于城市地下空间建设。获取精细的近地表结构特征及准确的参数模型(横波速度,纵波速度、品质因子Q参数等)是解决这些问题的关键。
现阶段地震数据物性参数反演存在挑战和技术难题包括:
(1)在面波反演方面,常规频散曲线反演基于一维层状介质假设,对于横向变化大的近地表复杂结构难以获得高分辨率的探测结果;面波全波形反演(FWI)在近地表低信噪比地震数据应用中具有挑战性,最新发展的多尺度、包络目标函数、频率域等改进FWI算法也难以完全克服子波估计差、初始模型依赖、目标函数非线性、周期跳跃等问题。
(2)在体波成像方面,由于近地表地震数据信噪比低,体波信号能量弱,反射波、散射波等信息难以获得稳定结果,前人主要采用折射波初至走时信息开展射线层析成像(Ray Tracing)以及波动方程(Wave-equation Tomography)反演等方法,浅表层速度结构难以获得高分辨率的成像效果;
(3)在品质因子(Q)估计方面,前人研究主要根据地震信号的振幅衰减系数与Q值的经验关系估计换算地下结构的平均Q值分布。另一方面,采用QFWI全波形反演方法对速度模型依赖较大,速度模型误差会导致反演无法收敛。
针对上述问题,公司李静教授与合作导师沙特卜杜拉国王科技大学Gerard Schuster教授在2016年首次提出了地震数据波动方程的“骨架反演”(Skeletonized)成像方法,采用Connective Function理论,建立物性参数与地震波场之间的联系,可针对性的解决上述横波速度、纵波速度及品质因子Q参数反演存在的问题。取得的主要成果介绍如下:
1.提出了主动源/被动源面波频散骨架横波速度反演理论并获得实际应用
为了自动获得稳定的面波频散信息,申请人开发了基于非监督机器学习--支持向量机(SVM)方法提取面波频散(Li et al, Geophysics Prospecting, 2020)。
(1)与一维频散曲线反演相比,基于波动方程的反演策略具有较高的分辨率,解决了一维反演层状介质假设的限制,对于复杂结构速度成像具有更高的成像精度相关成果发表在 GJI (Li and Schuster, 2017)。图1a,b为真实模型和初始模型,图1 d为一维频散反演结果,图1c为采用申请人提出的骨架反演结果。由图可见,骨架反演策略精确地反演了低速夹层。
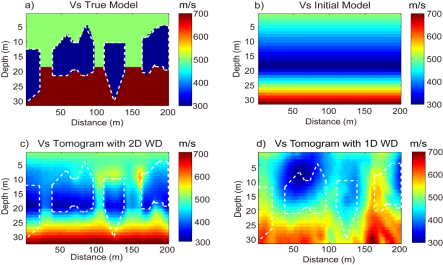
图1水平地表面波骨架全波形横波速度反演(Li and Schuster,GJI, 2017)
(2)骨架反演理论基于全波形地震数据中的“骨架”信息建立目标函数,只需要拟合反传骨架核心数据,降低了FWI方法中目标函数的非线性问题。另外,相比于全波形反演FWI,骨架反演理论的核心思想是保留地震数据中的核心(骨架)信息且忽略了在实测数据中难以匹配的全波信息(振幅等),使得反问题凸性更好。如此,虽然损失了一定的分辨率,但对于低信噪比的实测地震数据具有很好的鲁棒性。
前人研究表明,在地形起伏大于1倍波长条件下,面波频散曲线会出现较大的假异常。考虑到我国西部山区近地表地形条件异常复杂,申请人研发了二维、三维起伏地表面波骨架速度反演方法。通过模型测试和实测数据验证了该方法可以克服地形起伏的影响获得高精度的速度成像结果 (Li et al., GJI, 2019; Liu and Li., Geophysics, 2019, 2020)。
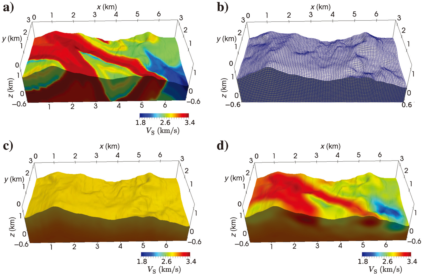
图2复杂三维山地横波速度模型反演.(a)真实模型;(b)有限元网格划分;(c)初始模型;(d)三维反演结果(Liu and Li,Geophysics, 2020)
2.提出了地震面波数据品质因子(Q)频移骨架反演方法获得高精度Q值估计
复杂近地表地质条件不但会影响采集参数选择,而且会引起地震波能量被强烈吸收和衰减,导致严重的静校正问题。与深部地层介质的吸收衰减效应相比,近地表介质对地震波高频成分的吸收衰减是降低地震资料分辨率的重要因素,近地表介质对地震波高频成分的吸收约占地层损耗总量的80%。申请人利用骨架反演思想,通过拾取地震信号频谱峰值频率作为骨架数据开展Q值波动方程骨架反演。理论模型和实测数据均验证了该方法对速度模型依赖低、在近地表Q值估计中具有较高的反演精度(Li et al, 2017, GJI)。


图3 骨架Q值反演模型测试.(a)单点炮集记录; (b)傅里叶变化频谱;(c)真实Q值分布模型; (d) Q值骨架反演结果(Li et al; 2017, GJI)
3.提出了地震体导波(Guided P-wave)反演方法获得高分辨率纵波速度成像
地震体波(P波)不具有面波的频散特性,常规近地表地震体波反演主要采用基于折射波初至时开展射线以及波动方程反演,其分辨率较低。在含有强速度界面的地下结构中,体波往往会在界面来回震荡,形成类似于谐振多次波的导波(Guided wave),称之为Guided P-wave。在天然地震断层研究中科学家称之为“沦陷波”(Trapped wave)。由于Guided P-wave存在多次谐振特征,根据谐振波的传导理论可获得小于1/3波长的目标分辨率(Grant and West, 1965)。申请人2018年首次提出了Guided P-wave骨架反演理论,并通过近地表实测数据验证了Guide P-wave可获得相比于走时反演更高分辨率的P波速度反演结果。图4是Guided P-wave的骨架反演流程,对比常规声波、弹性波波动方程走时成像(WT),导波反演方法具有更高的反演分辨率。
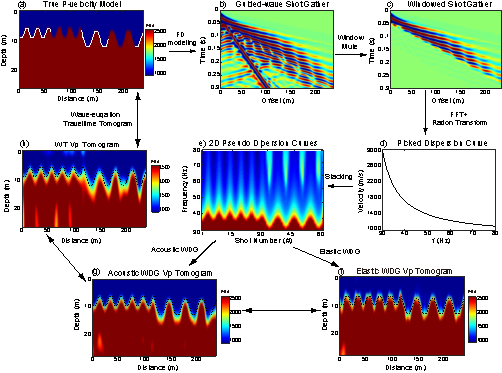
图4 Guided P-wave骨架反演流程及结果对比 (Li and Schuster, JGR, 2018)
上述成果分别发表在地球科学领域的顶级期刊《Journal of Geophysical Research: Solid Earth, JGR》《Geophysics Journal International, GJI》《Geophysics》《Scientific Reports》上。
1.Zhaoliu Liu, Jing Li*, Sherif Hanafy and Gerard Schuster, 3D wave-equation dispersion inversion of Rayleigh waves, Geophysics, 2019, 84(5): 1-127
2.Jing Li*, Zhaolun Liu, Sherif Hanafy and Gerard Schuster, Wave-equation dispersion inversion of Love waves, Geophysics, 2019, 84(5): 1-45.
3.Jing Li*, F-C Lin, Y. Benzion, A Alam, Z. Liu, GT Schuster. Wave-equation dispersion inversion of surface waves recorded on irregular topography, Geophysical Journal International, 2019, 217(1): 346-360.
4.Jing Li*, S Hanafy, GT Schuster. Dispersion inversion of guided P-waves in a waveguide of arbitrary geometry. Journal of Geophysical Research: Solid Earth, 2018,123, 9, 7760-7774.
6.Jing Li*, S Hanafy, GT Schuster, 2017. Parsimonious surface wave interferometry, Geophysical Journal International 212 (3), 1536-1545.
